Bloom-Filter beschleunigen in vielen Systemen die Zugriffszeiten. Sie wurden bereits 1970 entwickelt und finden in jüngerer Zeit vielseitige Verwendung, wenn es um die Optimierung von Systemen geht. Bloom-Filter finden viele Anwendungsgebiete, so unter anderem in LSM-Trees und damit in verteilten OLTP-Datenbanken. Wir untersuchen Bloom-Filter, entwerfen zuerst einen naiven Filter, um danach den eigentlichen Bloom-Filter zu beleuchten.
Ursprung von Bloom Filter
Burton H. Bloom veröffentlichte 1970 die Grundidee der heutigen Bloom Filter in seinem Paper “Space/Time Trade-offs in Hash Coding with Allowable Errors”
Als Beispielanwendung stellte er ein Programm vor, das in der Lage sein sollte, Trennzeichen in einem Text automatisch einzufügen. Dabei sollen die meisten Fälle mit ein paar einfachen Regeln erkannt werden und nur für die wenigsten Fälle ein teures Nachschlagen in einem Dictionary notwendig sein. Er geht davon aus, dass das Dictionary nicht ins Memory passt und Disk Zugriffe notwendig sind. Eine Hash-Struktur wäre viel kleiner und würde ins Memory passen. Könnte diese Hashstruktur ausgenutzt werden, um festzustellen, ob ein Wort im Dictionary vorkommt, dann wären unnötige Festplattenzugriffe vermeidbar.
So motiviert, entwickelt er in seinem Paper das Konzept, das heute als Bloom-Filter bekannt ist und vielseitig eingesetzt wird.
Seit 1970 haben sich die Größenordnungen geändert. Lösungsansätze, die seinerzeit wegen der knappen Ressourcen der damaligen Systeme entwickelt wurden, finden heute wieder Anwendung bei der Verarbeitung massiver Datenmengen.
Bloom-Filter werden in LMS-Datenbanken wie Google BigTable und Apache Cassandra verwendet, um festzustellen, ob es sich lohnt, in einer bestimmten SSTable überhaupt nach einem Key zu suchen. Jede SSTable wird von einem Bloom-Filter begleitet. Beim Lesen wird zuerst der Filter konsultiert – gibt er ein positives Ergebnis, dann wird die SSTable nach dem Key durchsucht.
Bloom-Filter werden gerne als probabilistische Datenstruktur bezeichnet. Das wird dadurch begründet, dass zu einem Bloom-Filter ein passender Hash-Algorithmus gehört und auch deshalb, weil False Positives möglich sind.
Ein sehr naiver Bloom-Filter und Murmur3
Wir stellen zuerst einen sehr naiven Bloom-Filter vor, um das Konzept zu erklären. Im folgenden Abschnitt werden wir diesen erweitern, so wie Bloom es in seinem Paper vorgeschlagen hat.
Die Struktur eines Bloom-Filters
Ein Bloom-Filter ist ein Bit-Array. Zu Beginn werden alle Bits auf 0 gesetzt.
Für jedes Element, beispielsweise für ein Key für eine SSTable, bestimmen wir einen Hashwert mit einer geeigneten Hashfunktion.
Wir erinnern uns an die wichtigsten Eigenschaften von Hash-Algorithmen:
- Durchläuft ein Wert einen Hash-Algorithmus mehrmals, dann ergibt sich immer derselbe Wert. Der Algorithmus ist also deterministisch.
- Aus dem Hash-Wert kann der Ausgangswert nicht eindeutig bestimmt werden.
- Und zwei Wert können denselben Hash-Wert haben.
Diese Eigenschaften sind Grundlage für das Funktionieren des Bloom-Filters.
Murmur3-Hash
Murmur3 ist eine geeignete Hashfunktion. Murmurhash wurde 2008 von Austin Appleby entwickelt – der Algorithmus wurde verbessert und liegt heute als Murmur3 vor: Hier die Referenzimplemenation: https://github.com/aappleby/smhasher
Im Wesentlichen werden bitweise Operationen wie Rotationen, Shift-Left und XOR durchgeführt. Murmur3 werden 32, 64, oder 128 Bit-Arrays erzeugen. Der Name Murmur ist abgeleitet von den wichtigsten Operationen: Multiply (also Shift-Left) und Rotate.
Beim Aufruf von Murmur3 geben wir einen Seed-Wert mit. Das ist eine ganze Zahl, mit der in der Folge die Multiplikationen und Rotationen beeinflusst werden.
Wollen wir mit Hilfe des so aufgebauten naiven Bloom-Filters prüfen, ob ein Key in unserem System vorhanden ist, dann bilden wir zuerst den Hashwert des Keys und verknüpfen dessen Bitfolge mit AND mit dem Filter. Resultiert der Key unverändert, dann können wir davon ausgehen, dass dieser in unserem System bereits bekannt ist.
Hier ein Code-Beispiel in Python für diesen naiven Bloom-Filter – wir benötigen dazu die mmh3 Library.
pip install mmh3
>>> import mmh3 >>> >>> h42=mmh3.hash('42', signed=False) >>> h42 3159925814 >>> bin(h42) '0b10111100010110001010010000110110' >>> >>> h53=mmh3.hash('53', signed=False) >>> h53 222179750 >>> bin(h53) '0b1101001111100011000110100110' >>> >>> # Den Filter erstellen >>> filter = h53 | h42 >>> bin(filter) '0b10111101011111101011010110110110' >>> >>> # Ist 42 im Filter vorhanden? >>> hq1=mmh3.hash('42', signed=False) >>> hq1 & filter == hq1 True >>> >>> # Ist 13 im Filter vorhanden >>> hq2=mmh3.hash('13', signed=False) >>> hq2 & filter == hq2 False >>>
Dabei kann es zu False Positive kommen – der Filter meint also, der Key sei in der SSTable, obwohl er dort nicht vorhanden ist.
Doch das ist nicht weiter schlimm – kommt es selten vor, dann wird die SSTable selten überflüssig durchsucht.
Mit diesem naiven Verfahren werden schon mit wenigen Keys alle Bits im Bloom-Filter auf 1 stehen: Das Beispiel zeigt einen 32-bit Bloom-Filter. Nur mit 2 Werten sind schon 22 der Bits auf 1 gesetzt. Es liegt auf der Hand, dass dieser kleine Bloom-Filter nicht effektiv ist, wenn wir mit sehr vielen Keys arbeiten müssen: – sehr schnell würden alle Bits auf 1 stehen und der Filter versagt.
Bloom-Filter – die Original-Idee
Auch der Original-Bloom-Filter ist ein Bit-Array. Dessen Länge kann je nach Bedarf unterschiedlich festgelegt werden.
Die Requisiten
Es kommen mehrere, voneinander unabhängige Hash-Algorithmen zum Zuge. Murmur3 wird ja mit einem Seed-Wert aufgerufen und mit verschiedenen Seed-Werten erhalten wir für ein und denselben Key jeweils verschiedene Hash-Werte.
Mit Murmur3 können wir diese Voraussetzung für einen Bloom-Filter mit nur einem Algorithmus erfüllen. Mehr als 12 verschiedene Hash-Algorithmen kommen selten zum Zuge.
Der Wertebereich der Hash-Funktion sollte die Länge des Bit-Array nicht übersteigen. Ist der Bit-Array kleiner als der Wertebereich der Hashfunktion, dann kann jeder Hashwert mit dem Modulo-Operator passend gemacht werden – einfach Hash-Wert modulo Array-Länge nehmen.
Das sind die Requisiten für den Bloom-Filter.
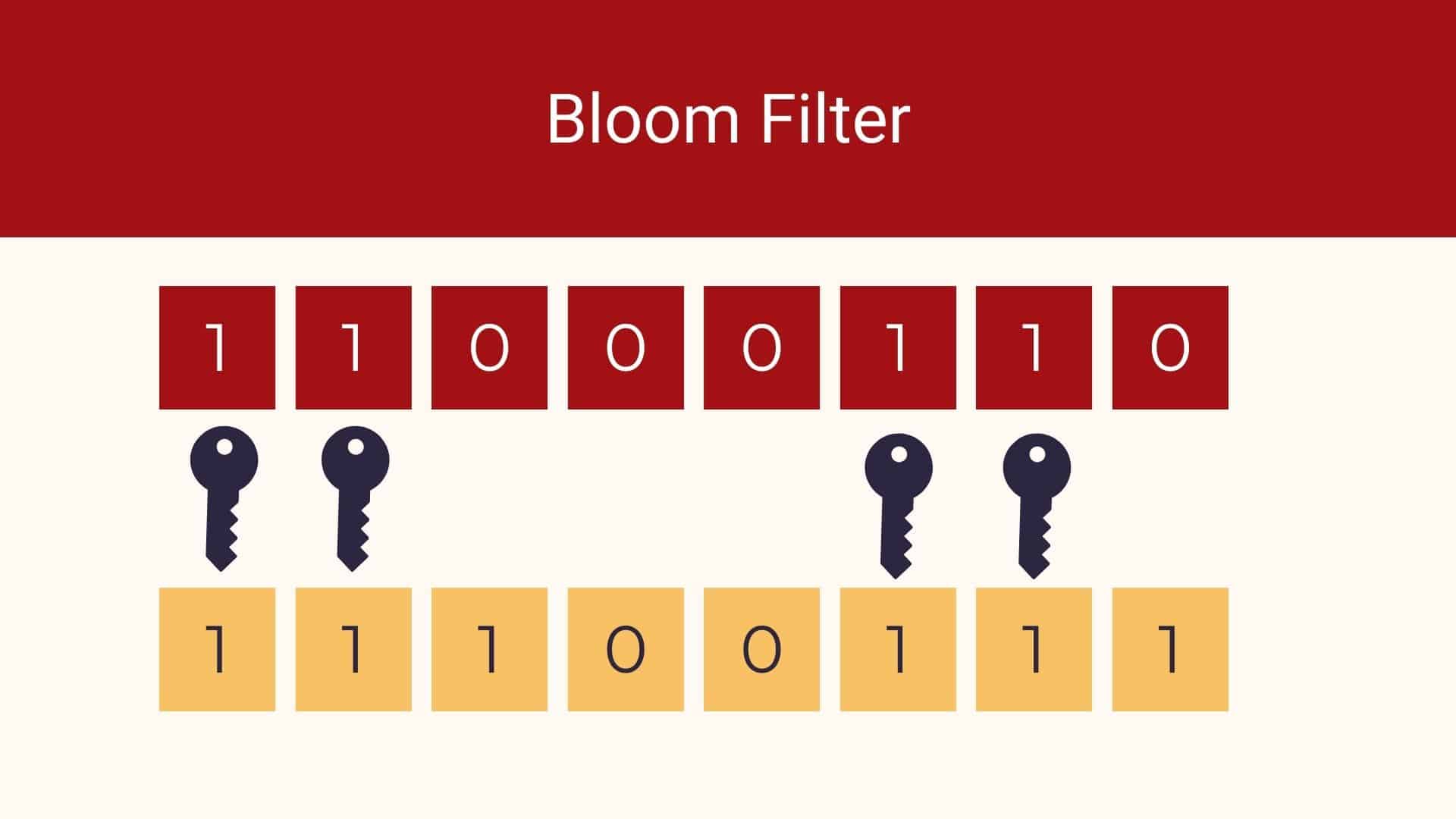
Einen Key in den Bloom-Filter einfügen
Wird ein Wert in den Bloom-Filter eingefügt, dann kommt der folgende Algorithmus zum Zug:
- Wiederhole für alle Hash-Funktionen:
- Für jede der Hash-Funktion resultiert eine Zahl, die als Index im Bit-Array des Bloom-Filters dient. Das entsprechende Bit wird auf 1 gesetzt.
Den Bloom-Filter befragen
Ist ein Key gegeben, und der Bloom-Filter soll die Frage beantworten, ob der Key in unserem System bereits bekannt ist, dann wird analog verfahren:
- Wiederhole für alle Hash-Funktionen:
- Bilde den Hashwert und prüfe, ob das entsprechende Bit im Array auf 1 gesetzt ist.
- Wenn für einen Hash-Operator das Bit auf 0 ist, dann ist der Wert sicher nicht in der Ursprungsmenge vorhanden.
- Wenn alle Hash-Operationen 1 liefern, dann ist die Wahrscheinlichkeit groß, dass der Wert in der Menge vorhanden ist.
- Bilde den Hashwert und prüfe, ob das entsprechende Bit im Array auf 1 gesetzt ist.
Wir sehen: je mehr Hashoperatioen zum Zuge kommen, um so verlässlicher arbeitet der Filter. Doch er wird damit auch langsamer.
Wie wir schon beim sehr naiven Bloom-Filter beobachten konnten, sind False Positives möglich. Es kann also sein, dass wir zu oft vergeblich in unserem System nach einem Key suchen werden.
False Negatives sind jedoch nicht möglich – wir werden wegen des Bloom-Filters keinen Key verpassen.
Fazit
Bloom-Filter eignen sich hervorragend, um die Mitgliedschaft eines Keys in einer Menge zu prüfen. Sie wurden bereits 1970 entwickelt und fanden in jüngerer Zeit Eingang in viele Systeme, um Zugriffszeiten zu optimieren.
Dieser Artikel ist ein Auszug aus dem E-Book Datenstrukturen für Data Engineers.






















